Silva desenhou as figuras a seguir na malha quadriculada a) considerando o lado (1) do quadrinho da malha como unidade de medida de comprimento, responda. qual é o perímetro do retângulo vermelho?e o perímetro verde?b) usando o quadradinho da malha como unidade de medida de área,responda:.qual é a área do retângulo vermelho?.qual é a área do retângulo verde?c) o que é possível concluir observando o perímetro e a área dos retângulos desenhados por Silva?

-
Assunto:
Matemática -
Autor:
wesley -
Criado em:
1 ano atrás
Respostas 1
Para q = unidade de medida quadradinhos:
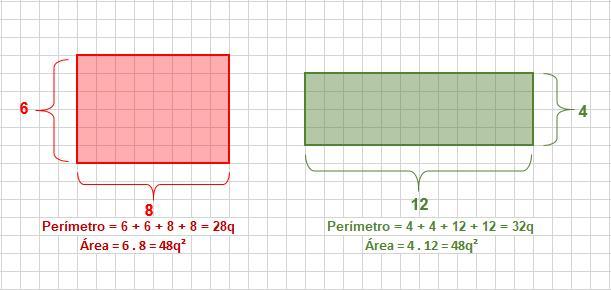
a) Perímetro retângulo Vermelho = 28 q
Perímetro retângulo Verde = 32 q
b) Área retângulo Vermelho = 48 q²
Área retângulo Verde = 48 q²
c) Apesar do perímetro do retângulo verde ser maior que o perímetro do vermelho, suas áreas são iguais. Isso acontece porque a quantidade de quadradinhos total de cada figura é a mesma.
Para esses resultamos vamos precisar das definições de:
→ Perímetro é a soma das medidas de todos os lados do polígono, ou seja, é a medida do contorno.
→ A área de um retângulo é dada pela multiplicação do complimento pela largura.
a)
⇒ P1 = Perímetro do retângulo Vermelho:
P1 = 2.6 + 2.8
P1 = 12 + 16
P1 = 28 q
⇒ P2 = Perímetro do retângulo Verde:
P2 = 2.4 + 2.12
P2 = 8 + 24
P2 = 32 q
b)
⇒ A1 = Área do retângulo Vermelho:
A1 = 6 . 8
A1 = 48 q²
⇒ A2 = Área do retângulo Verde:
A2 = 4 . 12
A2 = 48 q²
Obs.1.: Lembre sempre que para áreas usamos unidade de medidas ao quadrado.
c) Observando os perímetros e as áreas calculados, podemos concluir:
⇒ Apesar do perímetro do retângulo verde ser maior que o perímetro do vermelho, suas áreas são iguais. Isso acontece porque a quantidade de quadradinhos total de cada figura é a mesma.
Obs.2: Caso Silva desenhasse outro retângulo de, por exemplo,
2q de largura por 24q de comprimento ou outro de
3q de largura por 16q de comprimento
As áreas também seriam as mesmas, pois foram utilizados 48q para compor o desenho.
Veja mais sobre perímetros e áreas em:
https://brainly.com.br/tarefa/43550710
https://brainly.com.br/tarefa/10305166
-
Autor:
poochieqhwk
-
Avalie uma resposta:
2


