As séries telescópicas apresentam esse nome oriundo do fato de que na simplificação da soma, uma parcela cancela uma parcela próxima, ou seja, assim como um telescópio que encurta a enorme distância entre nossos olhos e os corpos celestes, essa propriedade encurta o caminho entre a soma inicial de muitas parcelas e o cálculo do resultado. Dessa forma, não é necessário desenvolver uma quantidade infinita de termos ou simplificar por muito tempo uma cadeia de adendos. Use as informações acima e prove que: (veja a imagem)
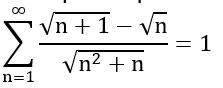
-
Assunto:
Matemática -
Autor:
adelynkirby -
Criado em:
1 ano atrás
Respostas 1
Resposta: A partir dos dados fornecidos pelo problema e dos devidos cálculos que realizaremos, é possível verificar que o valor da soma de todos os termos desta série telescópica é igual a 1.
- Vamos entender ou por quê?
Queremos mostrar que a seguinte série telescópica resultante da soma de todos os seus números é igual a 1, ou seja, que:
[tex]\displaystyle \sf \sum^{\infty} _{n=1} \dfrac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n^2+n}}=1[/tex]
Sabemos que a soma telescópica é um ramo das operações com séries numéricas. Aborda os somatórios de elementos de um valor inicial a "n" de expressões cujo argumento obedece a um padrão específico. À medida que se desenvolve, está sujeito a cancelamentos de termos opostos. Tornando possível definir a seguinte igualdade para somatórias telescópicas:
[tex]\displaystyle \sf \sum^{k} _{n=1} (a _ n+ a _{n + 1})= a _1 - a _{n +1}[/tex] (i)
Então, para provar essa igualdade, devemos simplificar nossa expressão para apenas uma adição ou subtração de frações com radicais, nossa soma telescópica pode ser escrita como:
[tex]\displaystyle \sf \sum^{\infty} _{n=1} \left(\dfrac{\sqrt{n+1}}{\sqrt{n^2+n}}-\dfrac{\sqrt{n}}{\sqrt{n^2+n}}\right)[/tex]
Podemos ver que nossa soma telescópica tem mais ou menos a mesma forma que a expressão (i), bastaria mudar a soma para infinito por k e simplificar um pouco essa expressão, para simplificar essa expressão vamos usar o leis dos radicais da seguinte maneira:
[tex]\displaystyle \sf \sum^{\infty} _{n=1} \left(\sqrt{\dfrac{n +1}{n^2+n}}-\sqrt{\dfrac{{n}}{{n^2+n}}}\right)\\\\\\\\ \displaystyle \sf \sum^{\infty} _{n=1} \left(\sqrt{\dfrac{n +1}{n(n+1)}}-\sqrt{\dfrac{{n}}{{n(n+1)}}}\right)[/tex]
Vamos simplificar a expressão, para simplificar esta expressão vamos cancelar os termos semelhantes da expressão, se eliminarmos os termos semelhantes obtemos:
[tex] \displaystyle \sf \sum^{\infty} _{n=1} \left(\sqrt{\dfrac{1}{n}}-\sqrt{\dfrac{{1}}{{n+1}}}\right)[/tex]
Podemos ver que essa soma está na forma de uma soma telescópica, então para encontrar o valor da soma de seus termos vamos mudar infinito para "k", pois se fizermos isso devemos demonstrar que existem termos opostos que pode ser cancelado. Avaliando nossa soma em "k" obtemos:
[tex] \displaystyle \sf \sum^{k} _{n=1} \left(\dfrac{1}{\sqrt{n}}-\dfrac{{1}}{{\sqrt{n+1}}}\right)= \left(1-\dfrac{1}{\sqrt{2}} \right)+ \left(\dfrac{1}{\sqrt{2}} -\dfrac{1}{\sqrt{3}}\right)+\left(\dfrac{1}{\sqrt{3}} -\dfrac{1}{2}\right)+\dots+\left(\dfrac{1}{\sqrt{k}}+\dfrac{1}{\sqrt{k+1}}\right)[/tex]
Se desenvolvermos esse senador com apenas os três primeiros termos do desenvolvimento, podemos ver que se houver termos opostos que possam ser cancelados, parece que apenas o primeiro e o último termo da soma não podem ser cancelados, então o resultado dessa soma é:
[tex] \displaystyle \sf \sum^{k} _{n=1} \left(\dfrac{1}{\sqrt{n}}-\dfrac{{1}}{{\sqrt{n+1}}}\right)=1 -\dfrac{1}{\sqrt{k+1}}[/tex] (ii)
Podemos ver que nosso resultado é o mesmo resultado que tínhamos que encontrar, pois apenas o primeiro termo menos o último termo é encontrado. Agora, para encontrar o valor desta mesma soma mas no infinito, é necessário avaliar a expressão (ii) no infinito, ou seja, deve ser avaliada em um limite ao infinito.
- Fazendo esta avaliação podemos ver que:
[tex] \displaystyle \sf S =\lim _{n \to\infty}1 -\dfrac{1}{\sqrt{n+1}}[/tex]
Pelas propriedades dos limites podemos traduzir esta equação como uma subtração de dois mesmos limites.
[tex] \displaystyle \sf S =\lim _{n \to\infty}1 -\lim _{n \to\infty}\dfrac{1}{\sqrt{n+1}}[/tex]
Para resolver um limite ao infinito devemos dividir a variável com o maior expoente em toda a nossa expressão, fazendo isso obtemos:
[tex] \displaystyle \sf S =\lim _{n \to\infty}1 -\lim _{n \to\infty}\dfrac{\frac{1}{n}}{\sqrt{\frac{n}{n}+\frac{1}{n}}}\\\\\\\\\displaystyle \sf S =\lim _{n \to\infty}1 -\lim _{n \to\infty}\dfrac{\frac{1}{n}}{\sqrt{1+\frac{1}{n}}} [/tex]
Avaliando todos os nossos limites no infinito e obtemos o seguinte resultado:
[tex] \sf S =1 -\dfrac{\frac{1}{\infty }}{\sqrt{1+\frac{1}{\infty }}}\\\\\\\\ \sf S = 1 -\dfrac{0}{\sqrt{1+0}}\\\\\\\\ \sf S =1-\dfrac{0}{1}\\\\\\\\ \sf S = 1 - 0\\\\\\\\ \boxed{\boxed{\sf S = 1}}\quad\longleftarrow\quad\mathsf {Comprovado!!}[/tex]
Conclusão: Feitos os cálculos, chegamos à conclusão de que o valor da soma desta série telescópica é igual a 1.
Bons estudos e espero que te ajude :-)
Duvidas? Comente
-
Autor:
bub3iod
-
Avalie uma resposta:
2
