Rafaela comprou três vestidos por 225 reais cada um e duas bolsas por 50 reais cada. ela vai pagar com 9 notas de 100reais. quanto ela vai receber de troco​

Resposta:

Explicação:

letra c:marcar explicação

Resposta:

Explicação:

Resposta:

requisitos

Explicação:

Resposta: Letra D; Projeto

Explicação: Projeto: uma vez tratados os requisitos, o modelo nos leva ao desenho do produto. Se os requisitos nos mostram o que o sistema deverá fazer, o projeto deverá refletir como ele o fará. Por meio do projeto, os requisitos são refinados de modo a se tornarem aptos a serem transformados em programa. O trabalho principal de um projetista é o de decompor o produto em módulos, que podem ser conceituados como blocos de código, que se comunicam com outros blocos por meio de interfaces (SCHACH, 2009).

Explicação:

O planeta Terra realiza dois movimentos principais. Em um primeiro movimento, chamado de translação, ela traça uma órbita em torno do Sol. Realiza também um giro em seu próprio eixo, chamado de rotação.

Cada volta ao redor do Sol representa um ano, enquanto cada giro em torno de seu próprio eixo define um dia.

O que é translação?

A translação é o movimento realizado pela Terra em torno do Sol. Isso ocorre pelo campo gravitacional gerado pela massa do Sol, fazendo com que a Terra fique presa a sua órbita.

O que é rotação?

A rotação é o movimento que a Terra faz em torno de seu próprio eixo. Cada giro da Terra ao redor de si mesma dura 23 horas, 56 minutos, 4 segundos e 9 centésimos. Por isso, convencionou-se que o dia tem vinte e quatro horas.

O eixo da Terra é uma linha imaginária que transpassa o planeta do polo norte ao sul. Esse eixo possui uma inclinação de cerca de 23,5 graus.

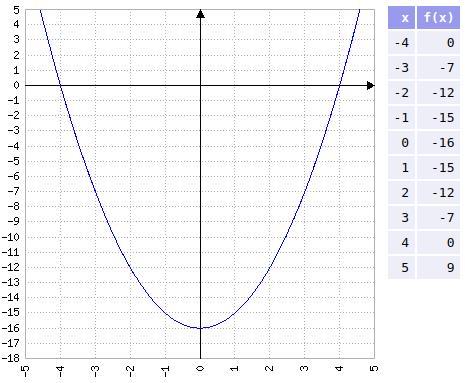
De acordo com os dados do enunciado e solucionado podemos afirmar que:

a) O vértice é o ponto V( 2, -16 );

b) Zeros da função: 6 e -2.

c) A figura em anexo.

A função quadrática (ou segundo grau), apresenta lei de formação y = f(x) = a.x² + bx + c, em a, b e c são os coeficientes da equação devendo ser números reais e a ≠ 0.

Zeros de uma função quadrática:

Os zeros ou raízes de uma função f(x) são os valores domínio para os quais f(x) = 0.

Vértice da parábola:

As coordenadas do vértice da parábola que representa a função do segundo f(x) =  ax² +bx +c é dada por:

[tex]\Large \displaystyle \text { $ \mathsf{ \begin{cases} \sf x_V = -\: \dfrac{b}{2a} \\ \\ \sf y_V = -\: \dfrac{\Delta }{4a} \end{cases} } $ }[/tex]

Dados fornecidos pelo enunciado:

[tex]\Large \displaystyle \text { $ \mathsf{ f(x) = x^{2} -4x -12 } $ }[/tex]

Resolução:

a) O vértice da função;

[tex]\Large \displaystyle \text { $ \mathsf{ x_V = -\: \dfrac{b}{2a} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x_V = -\: \dfrac{(-4)}{2\cdot 1} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x_V = \dfrac{4}{2} } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf x_V = 2 }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ y_V = -\: \dfrac{\Delta }{4a} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ y_V = -\: \dfrac{(b^{2} -4ac) }{4\cdot 1} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ y_V = -\: \dfrac{((-4)^{2} -4\cdot 1 \cdot (-12)) }{4\cdot 1} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ y_V = -\: \dfrac{(16 +48) }{4} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ y_V = -\: \dfrac{64 }{4} } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf y_V = -\: 16 }[/tex]

b) Os zeros da função;

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{-\,b \pm \sqrt{b^{2} -\, 4ac } }{2a} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{-\:(-4) \pm \sqrt{(-4)^{2} -\, 4 \cdot 1 \cdot (-12) } }{2 \cdot 1} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{4 \pm \sqrt{16 +48 } }{2 } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{4 \pm \sqrt{64} }{2 } } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ x = \dfrac{4 \pm 8 }{2 } \Rightarrow\begin{cases} \sf x_1 = &\sf \dfrac{4+8}{2} = \dfrac{12}{2} = \: \: 6 \\\\ \sf x_2 = &\sf \dfrac{4-8}{2} = \dfrac{- 4}{2} = - 2\end{cases} } $ }[/tex]

c) O esboço do gráfico da função:

Em anexo.

Mais conhecimento acesse:

https://brainly.com.br/tarefa/49414412

https://brainly.com.br/tarefa/53470288