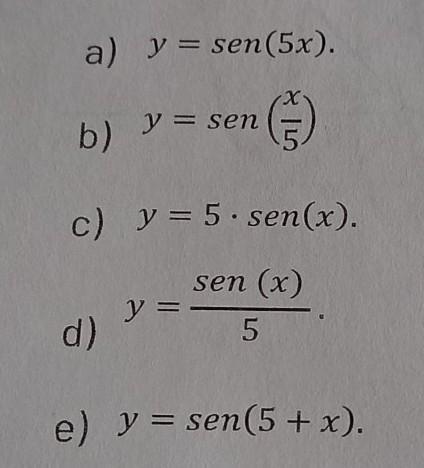Um determinado ângulo (a) possui o valor da sua tangente igual á 1, ou seja, tg (a) = 1. Nesse caso é possível afirmar que a) o valor do seno deste ângulo é 1 e o cosseno é 0. b) o valor do seno deste ângulo é 0 e o cosseno é 1. c) o valor do seno deste ângulo é igual ao cosseno em qualquer quadrante. d) o valor do seno deste ângulo é igual ao cosseno desde que estes ângulos estejam no 1° ou 3° quadrante. e) não é possível determinar.
-
Assunto:
Matemática -
Autor:
reidklein -
Criado em:
1 ano atrás
Respostas 2
É possível afirmar que o valor do seno deste ângulo é igual ao cosseno desde que estes ângulos estejam no 1° ou 3° quadrante, alternativa D.
Essa questão é sobre funções trigonométricas. As funções trigonométricas são obtidas a partir do circulo trigonométrico e são periódicas.
Estas funções também são muito úteis para estudar triângulos retângulos:
sen α = cateto oposto/hipotenusa;
cos α = cateto adjacente/hipotenusa;
tan α = cateto oposto/cateto adjacente;
Logo, podemos ver que a tangente de um ângulo nada mais é que a razão entre o seno e cosseno. Se a tangente é igual a 1, os valores de seno e cosseno são iguais:
tan α = sen α/cos α
1 = sen α/cos α
sen α = cos α
O seno e o cosseno possuem sinais iguais apenas no primeiro e terceiro quadrantes.
Leia mais sobre funções trigonométricas em:
https://brainly.com.br/tarefa/448151
https://brainly.com.br/tarefa/21757386
https://brainly.com.br/tarefa/25833272

-
Autor:
gallardods11
-
Avalie uma resposta:
7
Resposta:
d) o valor do seno deste ângulo é igual ao cosseno desde que estes ângulos estejam no 1° ou 3°
quadrante.
Explicação passo a passo:
-
Autor:
rambomoses
-
Avalie uma resposta:
2