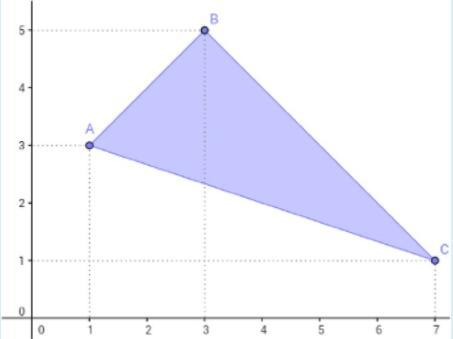
Determine a área, em metros quadrados, do triângulo a seguir, sabendo que ele é retângulo em B .

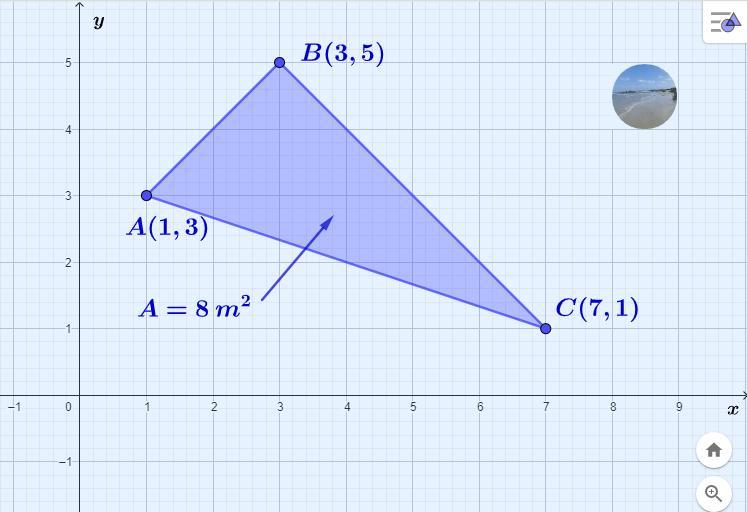
✅ Tendo terminado os cálculos, concluímos que a área do referido triângulo é:

   [tex]\Large\displaystyle\text{$\begin{gathered}\boxed{\boxed{\:\:\:\bf S_{\triangle} = 8\:m^{2}\:\:\:}}\end{gathered}$}[/tex]

Analisando a figura, concluímos que os vértices do respectivo triângulo são:

             [tex]\Large\begin{cases} A (1, 3)\\B (3, 5)\\C(7, 1)\end{cases}[/tex]

Como temos apenas os vértices do triângulo então podemos aplicar conceitos de geometria analítica para calcular sua área. Para isso, basta calcular a metade do módulo do determinante da matriz "M".

Se a matriz "M" é:

       [tex]\Large\displaystyle\text{$\begin{gathered}M = \begin{bmatrix} 1 & 3 & 1\\3 & 5 & 1\\7 & 1 & 1\end{bmatrix}\end{gathered}$}[/tex]

Então, temos:

       [tex]\Large\displaystyle\text{$\begin{gathered} S_{\triangle} = \frac{|\det M|}{2}\end{gathered}$}[/tex]

                [tex]\Large\displaystyle\text{$\begin{gathered}= \begin{vmatrix}1 & 3 & 1\\3 & 5 & 1\\7 & 1 & 1 \end{vmatrix} / 2\end{gathered}$}[/tex]

                 [tex]\Large\displaystyle\text{$\begin{gathered} = \left|\begin{vmatrix}5 & 1\\1 & 1 \end{vmatrix}\cdot 1 - \begin{vmatrix}3 & 1\\7 & 1 \end{vmatrix}\cdot3 + \begin{vmatrix} 3 & 5\\7 & 1\end{vmatrix}\cdot1\right|/2\end{gathered}$}[/tex]

                  [tex]\Large\displaystyle\text{$\begin{gathered} = \left\|(5 - 1)\cdot1 - (3 - 7)\cdot3 + (3 - 35)\cdot1\right\| / 2\end{gathered}$}[/tex]

                  [tex]\Large\displaystyle\text{$\begin{gathered} = \left\|4\cdot1 - (-4)\cdot3 + (-32)\cdot1\right\| / 2\end{gathered}$}[/tex]

                   [tex]\Large\displaystyle\text{$\begin{gathered} = |4 + 12 - 32| /2\end{gathered}$}[/tex]

                   [tex]\Large\displaystyle\text{$\begin{gathered} = |-16| / 2\end{gathered}$}[/tex]

                   [tex]\Large\displaystyle\text{$\begin{gathered} = 16/2\end{gathered}$}[/tex]

                    [tex]\Large\displaystyle\text{$\begin{gathered} = 8\end{gathered}$}[/tex]

✅ Portanto, a área do triângulo é:

              [tex]\Large\displaystyle\text{$\begin{gathered} S_{\triangle} = 8\:m^{2}\end{gathered}$}[/tex]

[tex]\LARGE\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Bons \:estudos!!\:\:\:Boa\: sorte!!\:\:\:}}}\end{gathered}$}[/tex]

Saiba mais:

1. https://brainly.com.br/tarefa/49368580
2. https://brainly.com.br/tarefa/49693403
3. https://brainly.com.br/tarefa/39857279
4. https://brainly.com.br/tarefa/51803980
5. https://brainly.com.br/tarefa/46916311

[tex]\Large\displaystyle\text{$\begin{gathered} \underline{\boxed{\boldsymbol{\:\:\:Observe \:o\:Gr\acute{a}fico!!\:\:\:}}}\end{gathered}$}[/tex]

A área do triângulo é 8 m².

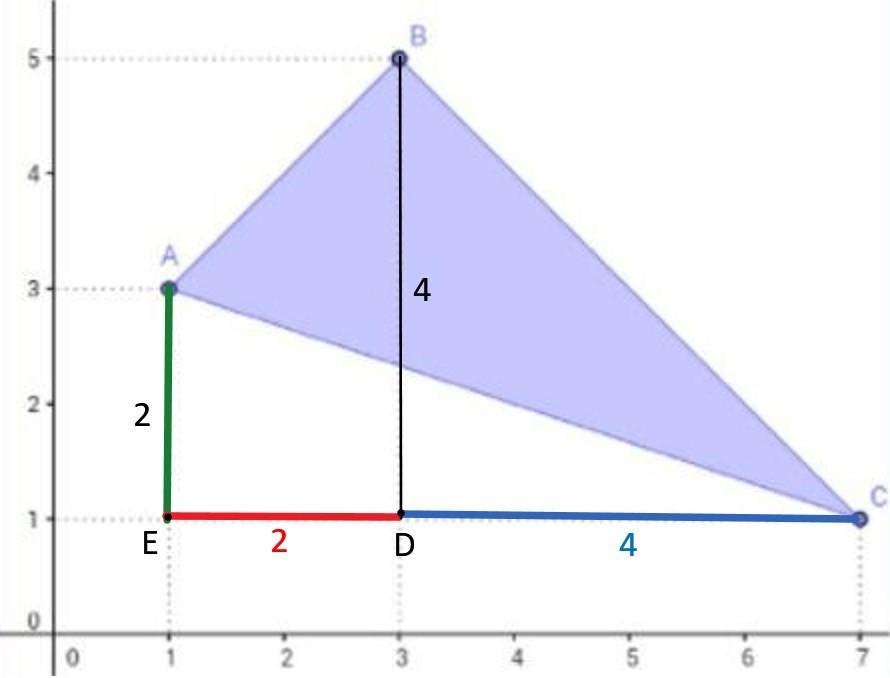
• Observe na imagem anexa que a área (A) do triângulo ABC corresponde à área do trapézio ABDE mais a área do triângulo BCD menos a área do triângulo ACE, cujas medidas são:

Trapézio ABDE: Base maior = 4m, base menor = 2m e altura = 2 m.

Triângulo BCD: Catetos medindo 4 m.

Triângulo ACE: Catetos medindo 2m e 6 m

[tex]\large \text {$ \sf A = \dfrac{(4+2) \cdot 2}{2} + \dfrac{4 \cdot 4}{2} - \dfrac{6 \cdot 2}{2}$}[/tex]

A = 6 + 8 − 6

A = 8 m²

A área do triângulo é 8 m².

Aprenda mais em:

• brainly.com.br/tarefa/38207158
• brainly.com.br/tarefa/36043042
• brainly.com.br/tarefa/33666768
• brainly.com.br/tarefa/31918282
• brainly.com.br/tarefa/30353414