O relógio a seguir está marcando 3 horas. O menor ângulo formado pelos ponteiros e (A) obtuso (B) agudo (C) raso (D) reto​

Resposta:

Rigorosamente, são três os modos verbais: INDICATIVO, SUBJUNTIVO e IMPERATIVO. ... Porém, alguns gramáticos incluem, também como modos verbais, o PARTICÍPIO, o GERÚNDIO e o INFINITIVO. Alguns autores, no entanto, as denominam FORMAS NOMINAIS DO VERBO.

Explicação:BRINLY LINDO E MUITO BOM ESSE APLICATIVO ME AJUDOU DE MAIS VALEU

d) o movimento é retardado e F1 + F2 cos θ = mα.O movimento é retardado, a resultante F1 e F2 (seta pra direita em cima dos F) na direção tangencial é oposta ao vetor V(seta pra direita em cima do V). f=m.a

Resposta:

A figura mostra os três retângulos diferentes que podem ser construidos com 12 quadrados iguais. Quantos retângulos diferentes podem ser construidos com 60 quadrados iguais? *

Gabaritei, seu quiser ar como melhor resposta, agradeço

Resposta: B) 6

Podem ser construídos seis retângulos diferentes com 60 quadradinhos iguais.  

Vamos encontrar todos os divisores de 60. Eles são 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.  

Dado que a área de um retângulo é igual ao produto da base e da altura, os diferentes produtos são:  

1·60, 2·30, 3·20, 4·15, 5·12 e 6·10

Podem ser construídos 6 retângulos com 60 quadradinhos iguais!

Explicação passo a passo:

Podem ser construídos 6 retângulos diferentes com 60 quadrados iguais.

Alternativa B.

• Observe que para determinar a quantidade de retângulos que podem ser construídos com 12 quadrados é necessário obter fatores cujo produto é 12, que são:

1 × 12 = 12

2 × 6 = 12

3 × 4 = 12

• Para determinar a quantidade de retângulos que podem ser construídos com 60 quadrados determine os fatores cujo produto é 60:

1 × 60 = 60

2 × 30 = 60

3 × 20 = 60

4 × 15 = 60

5 × 12 = 60

6 × 10 = 60

• Observe portanto que há 6 possíveis retângulos diferentes que podem ser construídos com 60 quadrados iguais.

Resposta: alternativa B.

Aprenda mais em:

• https://brainly.com.br/tarefa/43794739
• https://brainly.com.br/tarefa/34234384

Resposta:

D) 1536

Explicação passo a passo:

Acho que é essa, vou colocar na minha prova

Resposta:

É possível fazer isso de 1 536 maneiras diferentes.

Explicação passo a passo:  

Para conseguirmos descobrir de quantas maneiras diferentes é possível encaixar as peças, devemos nos atentar aos mínimos detalhes fornecidos pelo enunciado e analisar a imagem anexada.  

Sendo assim ao analisar o texto e a imagem, nota-se que:

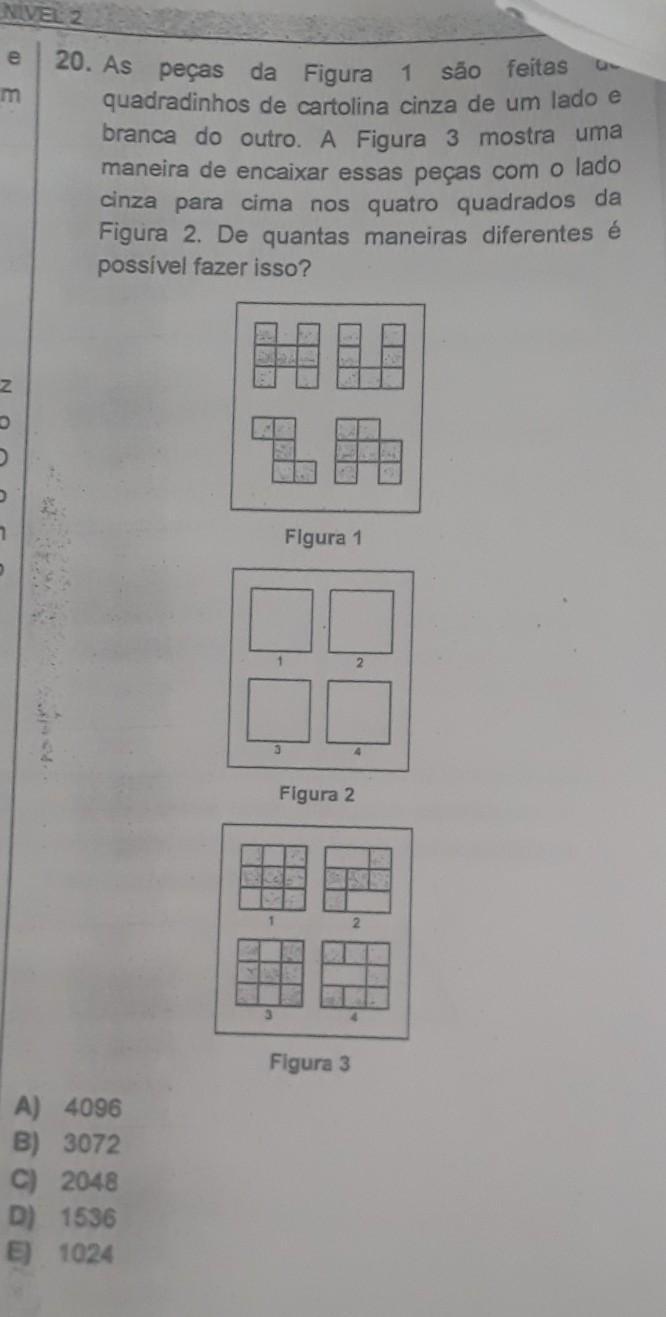
Temos 4 peças diferentes e essas peças são formadas por quadradinhos (Figura 1);

Temos 4 quadrados idênticos (Figura 2);

As peças da figura 1 devem ser encaixadas nos quadrados da figura 2 e podem ser encaixadas de diferentes modos como demonstra a figura 3.

Desse modo, para resolvermos a questão, devemos analisar peça por peça:

Primeira peça de cima (Parecida com um H): pode ser encaixada de duas formas diferentes;

Segunda peça de cima (Parecida com um U): pode ser encaixada de quatro formas diferentes;

Terceira peça de baixo (Parecida com um Z): pode ser encaixada de duas formas diferentes;

Quarta peça de baixo (Parecida com um R): pode ser encaixada de quatro formas diferentes;

Em seguida devemos descobrir de quantas formas diferentes é possível distribuir as 4 peças nos quatro quadrados:

Para o primeiro quadrado temos 4 opções de peça, para o segundo temos 3, pois uma já foi colocada no primeiro, e seguindo esse raciocínio temos 2 peças para o terceiro e 1 peça para o quarto.

Sendo assim, para descobrir de quantas formas diferentes podemos distribuir as peças devemos fazer a seguinte multiplicação: 4 x 3 x 2 x 1 =  24. Ou seja, existem 24 formas diferentes de distribuir as peças nos quatro quadrados da figura 2.

Por fim, devemos multiplicar 24 pela quantidade de formas diferentes que as peças podem ser encaixadas, a fim de descobrir de quantas maneiras diferentes é possível encaixar as peças. Sendo assim, temos: 2 x 4 x 2 x 4 x 24 = 1536.