Faetec* PRECISO DO CÁLCULO DESSA QUESTÃO, pfvr me ajudem é para amanhã
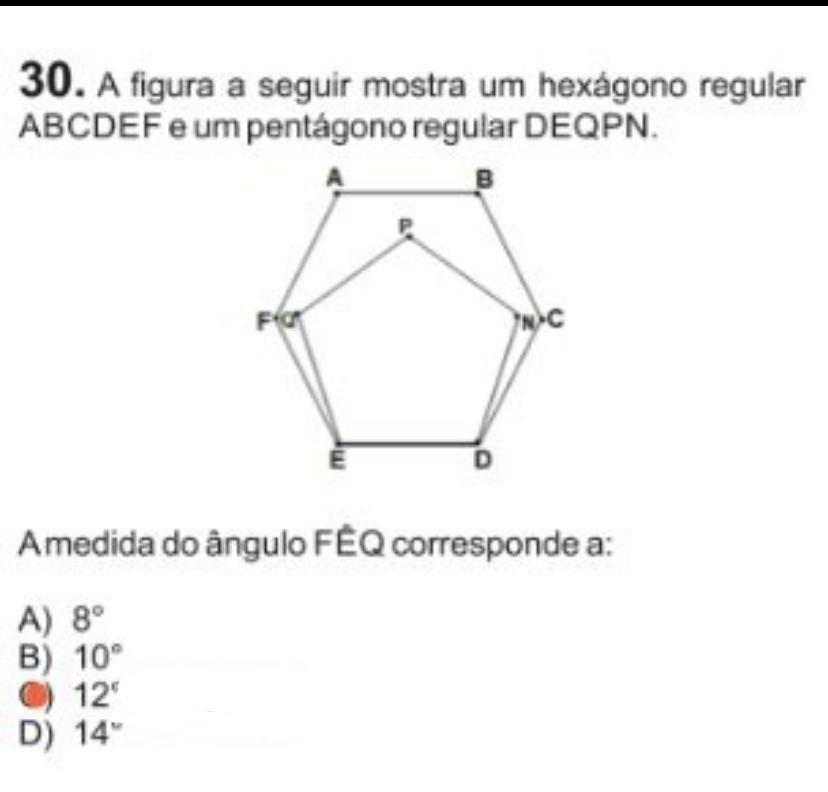
-
Assunto:
Matemática -
Autor:
graysontran -
Criado em:
1 ano atrás
Respostas 1
Resposta:
12°
Explicação passo-a-passo:
A soma dos ângulos internos de um polígono é dada pela expressão:
S = (n – 2 )*180º, onde n = número de lados.
Hexágono ABCDEF:
S = (6-2)*180°
S = 4*180°
S = 720°
Logo 720°/6 = 120° , cada ângulo tem 120°
Fazendo para DEQPN:
S = (5-2)*180°
S = 3*180°
S = 540°
540°/5 = 108°, cada ângulo do pentágono tem 108°
Por fim, a medida do ângulo FÊQ = 120° - 108° = 12°
-
Autor:
julianyg19
-
Avalie uma resposta:
1
Você sabe a resposta? Adicione-a aqui!
Escolha um idioma e uma região
How much to ban the user?
1 hour
1 day
100 years
