Cite três músicas com gírias​

Resposta:

Explicação:

a) A estratégia aplicada pelos entrevistadores do jornal, foi o uso de palavras e expressões informais durante a apresentação do tema da reportagem.

b) O que os divertiu, foi o uso de gírias e expressões em um ambiente formal, onde geralmente os mesmos não podem usá-las.

c) Sim, o texto de apresentação demonstrou através da exemplificação as diversas variações da língua portuguesa.

d) A iniciativa da repórter Anna Zimmerman comprova seu argumento. E demonstra que a variação linguística realmente ocorre e varia entre as regiões.

E) A expressão "língua que a gente fala" refere-se a linguagem informal utilizada no cotidiano pelas pessoas. É o tipo de linguagem que foge da norma culta.

f) As marcas de oralidade vistas durante a apresentação da reportagem, está associada a fala de gírias, sotaques e expressões regionais.

São chamadas de expressões regionais, o vocabulário regional marcado pelo uso de gírias populares.

Acesse mais questões sobre expressões regionais e linguagem informal em:

https://brainly.com.br/tarefa/17897588?utm_source=android&utm_medium=share&utm_campaign=question

Bons estudos!

A área total do cilindro é de 80π - alternativa D.

• Explicação:

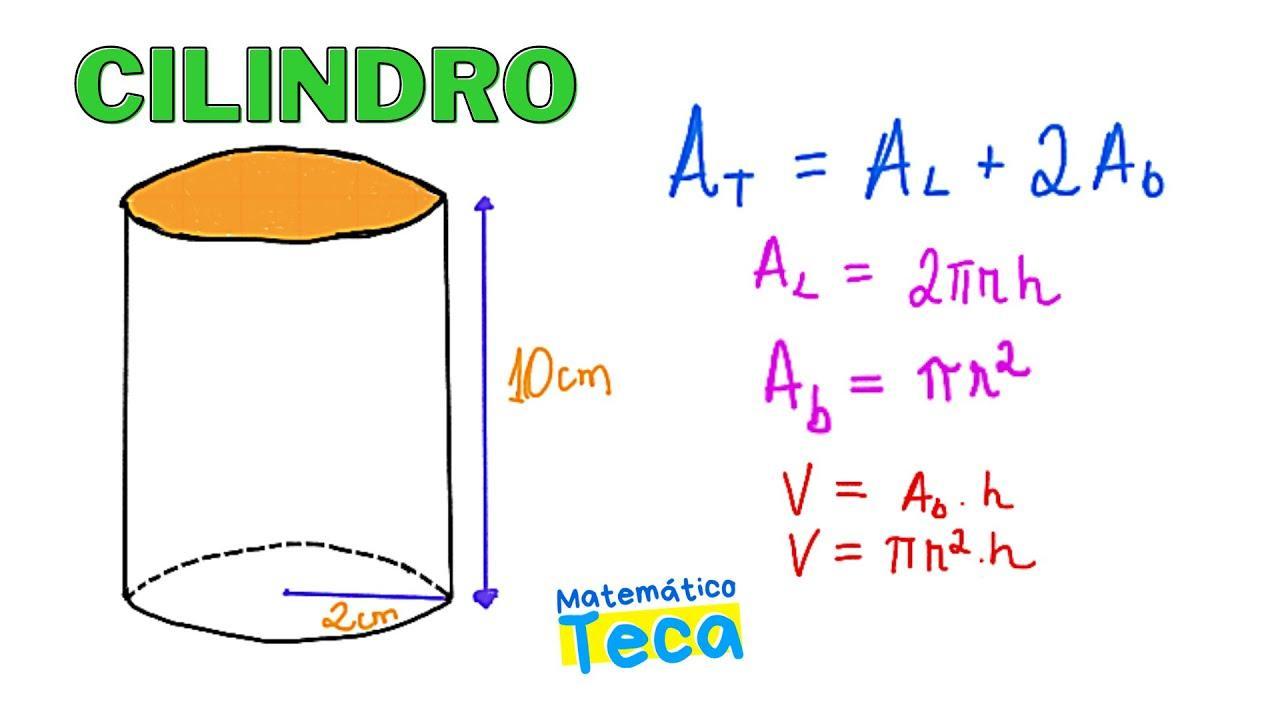
A questão aborda diferentes aspectos da geometria espacial. Faremos vários cálculos diferentes nessa questão, então resolveremos por partes.

1. Achar a altura do cilindro

A altura equivale à aresta do cubo de área total 216 cm². Então primeiro vamos achar a aresta em questão:

[tex]\bf A_t = 6 \cdot a^{2}[/tex]

[tex]\bf 216 = 6 \cdot a^{2}[/tex]

[tex]\bf a^{2} = \dfrac{216}{6}[/tex]

[tex]\bf a^{2} = 36[/tex]

[tex]\boxed {\bf a = 6 \ cm}[/tex]

Se a aresta do cubo vale 6 cm, a altura H do cilindro também vale 6 cm.

2. Achar o raio da base do cilindro

[tex]\bf V = \pi \cdot r^{2} \cdot H[/tex]

[tex]\bf 96 \pi = \pi \cdot r^{2} \cdot 6[/tex]

[tex]\bf r^{2} = \dfrac{96 \pi}{6 \pi}[/tex]

[tex]\bf r^{2} = 16[/tex]

[tex]\boxed {\bf r = 4 \ cm}[/tex]

O raio da base do cilindro vale 4 cm.

3. Achar a área total do cilindro:

[tex]\bf A_t = 2 \cdot A_L + A_b[/tex]

[tex]\bf A_t = 2 \cdot \pi r^{2} + 2 \cdot \pi \cdot r \cdot H[/tex]

[tex]\bf A_t = 2 \cdot \pi \cdot 4^{2} + 2 \cdot \pi \cdot 4 \cdot 6[/tex]

[tex]\bf A_t = 2 \cdot \pi \cdot 16 + 2 \cdot \pi \cdot 4 \cdot 6[/tex]

[tex]\bf A_t = 32 \cdot \pi + 48 \cdot \pi[/tex]

[tex]\boxed {\bf A_t = 80 \cdot \pi}[/tex]

➯ A área total do cilindro é de 80π cm² -  alternativa correta letra D.

Saiba mais sobre geometria espacial em:

https://brainly.com.br/tarefa/1446713

Espero ter ajudado!

Na imagem do campo eólico, pode-se observar exemplos de matéria como:  Turbinas eólicas, ar, Sol, solo, água, e vegetação.

Questão 1: A matéria é o componente principal dos corpos, suscetível a todos os tipos de formas e a sofrer alterações, caracterizado por um conjunto de propriedades físicas ou químicas, perceptíveis através dos sentidos.

Questão 2: Exemplos de Transformação da energia são:

• Energia luminosa ⇒ Energia térmica: raios solares que aquecem o ambiente;

• Energia mecânica ⇒ Energia elétrica: a energia do vento sendo transformado pelas turbinas em eletricidade;

• Energia luminosa ⇒ Energia química: raios solares sendo transformados pela vegetação, através da fotossíntese, em seu alimento.

Questão 3: a matéria pode sofrer transformações físicas e químicas.

Questão 4: Observando a imagem temos que:

• Componentes vivos: as plantas;
• Componentes não vivos: areia, ar, água, turbinas eólicas.

Componente vivo é aquele pode realizar as funções básicas de se nutrir, desenvolver, reproduzir, respirar, etc., já que eles possuem células, metabolismo, respostas a estímulos, entre outras características que estão ausentes nos componentes não vivos

Entenda mais sobre a energia eólica em: https://brainly.com.br/tarefa/25788573

Resposta:

eu botei a letra C

Explicação:

espero te ajudado