Paroxítona oxítona ou paroxítona Lâmpada Café Caneca Prato Mesada Números Mulheres Dominó Lampião Refeição Sofá Matemática

A tradição é um dos meios de manutenção da cultura, mas pode também ser usada para a manutenção do poder opressivo regente e direcionado a certa porcentagem da população.

As funções atribuídas em sociedade, tradicionalmente leva às mulheres ao processo de submissão, subserviência aos seus esposos, educação dos filhos, ao "matrimônio", modo contrário ao "patrimônio", assim também é responsável pelosos afazeres domésticos e uma vida regrada aos valores religiosos, “bons costumes”.

No passado, mulheres eram impedidas de estudar, votar, porque segundo diziam "seria o fim da sociedade moral" e também não se podia ter uma carreira profissional, pois isso a faria dona de seu próprio "patrimônio".

As constituições mundiais com ideais de participação civil e democrática, concorda, com a lógica dos direitos humanos, colocam a igualdade como fundamental independentemente de gênero, etnia, crença ou qualquer outro fator.

A respeito do texto, segue em anexo.

Para lermos mais a respeito da luta feminina, podemos acessar: https://brainly.com.br/tarefa/25070320

#SPJ4

Com base nos indicadores referentes ao ano de 2001 apresentados, o IDH do Brasil em 2003 foi de 0,777.

Para o cálculo do IDH de um país, são necessários os seguintes índices:

• Iesp = (esperança de vida ao nascer - 25) ÷ 60
• Ipib = (log PIB per capita - log 100) ÷ (log 40000 - log 100)
• Ico = (2/3 . taxa de alfabetização) + (1/3 . taxa de matrícula)

Dados esperança de vida ao nascer = 67,8, PIB per capita = 7360, taxa de alfabetização = 0873 e taxa de matrícula = 0,95, temos:

• Iesp = (67,8 - 25) ÷ 60 = 42,8 ÷ 60 = 0,713
• Ipib = (log 7360 - log 100) ÷ (log 40000 - log 100) = (3,87 - 2) ÷ (log 4,6 - 2) = 1,866 ÷ 2,6 = 0,717
• Ico = (2/3 . 0,873) + (1/3 . 0,95) = 0,582 + 0,317 = 0,899

Vamos, então, ao cálculo do IDH:

IDH = (1/3 . Iesp) + (1/3 . Ipib) + (1/3 . Ico) = (1/3 . 0,713) + (1/3 . 0,717) + (1/3 . 0,899) = 0,238 + 0,239 + 0,3 = 0,777

Aprenda mais sobre o Índice de Desenvolvimento Humano: https://brainly.com.br/tarefa/44678427

#SPJ4

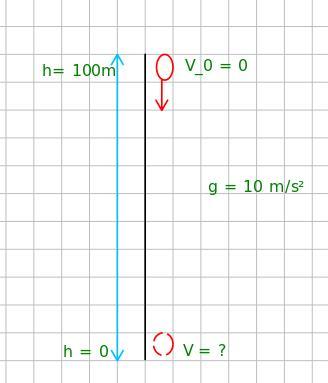
Após conhecermos o resultados do cálculos concluímos que  a velocidade desse corpo ao atingir o solo é de [tex]\textstyle \sf \text {$ \sf V = 20\: \sqrt{5} \:\: m/s $ }[/tex].

Forças conservativas realizam o mesmo trabalho,transformam energia potencial em energia cinética para qualquer caminho e não há perdas de energia.

Dados fornecidos pelo enunciado:

[tex]\Large \displaystyle \text { $ \mathsf{ \begin{cases} \sf m = 250\: kg \\ \sf V_0 = 0 \\ \sf h = 100 \: m\\\sf g = 10\: m/s^{2} \\\sf V = \:?\: m/s \\ \sf h_{solo} = 0 \end{cases} } $ }[/tex]

Resolução:

A energia do sistema se conserva

[tex]\Large \displaystyle \text { $ \mathsf{E_{M_A} = E_{M_B} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ E_C +E_P = E_C +E_P } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \dfrac{m \cdot V_0^2}{2} + m \cdot g \cdot h = \dfrac{m \cdot V^2}{2} + m \cdot g \cdot h_{solo} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \dfrac{ 250 \cdot 0^2}{2} + 250 \cdot 10 \cdot 100 = \dfrac{250 \cdot V^2}{2} + 250 \cdot 10 \cdot 0 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \dfrac{ 250 \cdot 0}{2} + 250 \cdot 10 \cdot 100 = \dfrac{250 \cdot V^2}{2} + 0 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 0 + 250 \cdot 10 \cdot 100 = \dfrac{250 \cdot V^2}{2} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ \backslash\!\!\!{ 2} \backslash\!\!\!{ 5}\backslash\!\!\!{ 0} \cdot 10 \cdot 100 = \dfrac{ \backslash\!\!\!{ 2} \backslash\!\!\!{ 5}\backslash\!\!\!{ 0} \cdot V^2}{2} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 10 \cdot 100 = \dfrac{ V^2}{2} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ 1\:000 = \dfrac{ V^2}{2} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{V^2 = 1\:000 \cdot 2 } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ V = \sqrt{2\:000} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ V = \sqrt{400 \cdot 5} } $ }[/tex]

[tex]\Large \displaystyle \text { $ \mathsf{ V = \sqrt{400} \: \cdot \sqrt{5} } $ }[/tex]

[tex]\Large \boldsymbol{ \displaystyle \sf V = 20 \:\sqrt{5} \: m/s }[/tex]

Mais conhecimento acesse:

https://brainly.com.br/tarefa/50297892

https://brainly.com.br/tarefa/50705086

https://brainly.com.br/tarefa/50800412

A velocidade de propagação da onda transversal no fio é 5,65 m/s e sua tração é de 15,97 N.

A lei de Taylor demonstra a relação existente entre a força aplicada na corda, a densidade linear da mesma e a velocidade adquirida por ela em uma determinada oscilação.

• Resolução da letra a)

Para determinar a velocidade de propagação, podemos utilizar a seguinte relação do movimento circular:

v  = ω.R

Onde ω é a frequência angular, que pode ser calculada na maneira a seguir:

ω  = 2π.30

ω = 2π . 30

ω = 188,4 rad/s

Assim, substituindo na equação anterior, temos:

v = 188,4 . 0,03

v = 5,65 m/s

• Resolução da letra b)

A lei de Taylor matematicamente é expressa como:

v = [tex]\sqrt{\frac{T}{d}}[/tex]

Onde d é a densidade linear, definida a seguir:

d = m/l

Assim, substituindo na equação anterior, temos:

v = [tex]\sqrt{\frac{T.l}{m} }[/tex]

Por fim, reorganizamos os termos desta equação do seguinte modo:

T = [tex]\frac{v^2.m}{l}[/tex]

T = [tex]\frac{5,65^2.0,3}{0,6}[/tex]

T = 15,97 N

Leia mais sobre movimento circular em https://brainly.com.br/tarefa/7336966

#SPJ4