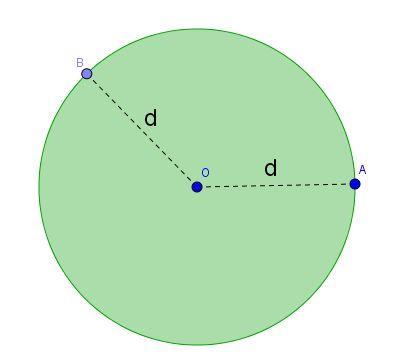
O número irracional π pode ser obtido por meio de uma relação entre duas medidas de uma mesma circunferência.Uma relação pela qual se obtém esse número π é aa) razão entre a medida do comprimento e do raio da circunferência.b) razão entre a medida do comprimento e do diâmetro da circunferência.C) razão entre a medida do diâmetro e do comprimento da circunferência.d) diferença entre a medida do comprimento e do raio da circunferência.e) diferença entre a medida do comprimento e do diâmetro da circunferência.

Resposta:

R$15,00

Explicação passo-a-passo:

colocaremos o valor do refresco como X e o valor da sobremesa como Y

[tex]27 = 16 + 2x + y \\ 35 = 16 + 3x + 2y[/tex]

resolvendo a conta, nós temos

X = 3 e Y = 5

para descobrir o total que eles gastaram, iremos multiplicar com o valor de X aplicado

[tex]2x = 2 \times 3 = 6 \\ 3x = 3 \times 3 = 9 \\ assim \\ 6 + 9 = 15[/tex]

O total gasto com refresco foi igual a R$ 15,00.

Conforme é apresentado pela questão, o valor fixo da refeição é igual a R$ 16,00, além disso, a quantidade de refrescos e quantidade sobremesas, em ordem, consumidas por Davi e Juliana foram: 2 e 1 e 3 e 2. Também, o total de Davi foi de R$ 27,00 e o total de Juliana foi de R$ 35,00.

Primeiramente, deve-se calcular o valor pago sem o valor fixo da refeição, para isso é preciso realizar as seguintes subtrações:

• Davi: 27 - 16 = 11;
• Juliana: 35 - 16 = 19.

Considerando x como o preço do refresco e y como o preço da sobremesa, tem-se o seguinte sistema de equações:

[tex]\left \{ {{2x+y=11} \atop {3x+2y=19}} \right.[/tex]

Multiplicando a primeira equação por 2 para simplificar y:

[tex]\left \{ {{4x+2y=22} \atop {3x+2y=19}} \right.[/tex]

Subtraindo as equações:

[tex]x=22-19=3[/tex]

Como a quantidade de refresco foi 5, pois 2 + 3 = 5, então o total gasto com refresco foi:

[tex]3\cdot 5 = 15[/tex]

Veja mais sobre sistema de equações em: https://brainly.com.br/tarefa/24392810

Resposta:

LETRA C

Explicação passo a passo:

350x10 = 3.500

3.500x3 = 10.500

Em um dia de treino, Miguel percorre 21000 metros.

O comprimento de uma região limitada por uma circunferência, ou seja, com formato circular é calculada através da expressão:

C = 2 · π · r

Em que C representa o comprimento da região e r representa o raio da região, ambos dados em metros.

Daí, segue que o comprimento da pista de corrida na qual Miguel pratica atletismo é a seguinte:

C = 2 · π · r

C = 2 · 3 · 350

C = 2100 metros

Se Miguel, a cada dia de treino, percorre 10 voltas nessa pista, então em um dia de treino, Miguel percorre 2100 · 10 = 21000 metros.

Mais sobre comprimento de uma região circular em:

https://brainly.com.br/tarefa/41553153

https://brainly.com.br/tarefa/37366997

Resposta:

b) a propriedade de cada atomos

Explicação:

na equação está demonstrando, cada propriedade de cada atomo. (espero ter ajudado).

Resposta:

letra B

Explicação:

Resposta:

Oie tudo bem?

Tô achando que é "Nem pegao passaporte" (3°estrofe)

Explicação:

Mais óbvia pra mim, pois complemento verbal fala sobre objeto direto é indireto.

Há um complemento verbal em:

“Nem pega o passaporte...”

Trata-se do termo "o passaporte", que é complemento do verbo "pega".

Note que o verbo "pegar" exige complemento, pois sozinho não tem sentido completo (pegar o quê?). Assim, o termo "o passaporte" complementa seu sentido.

Nessa questão, há uma inadequação, pois na frase "Aliás, não há destino" também há complemento verbal. Trata-se do termo "destino", que funciona como objeto direto do verbo "haver". Esse é um verbo impessoal quando tem sentido de existir, logo não admite sujeito. Por isso, o termo "destino" NÃO é sujeito dessa oração.

Mais sobre complemento verbal em:

brainly.com.br/tarefa/51860016