ESCOLHA OUTRA LENDA FOCLÓRICA E ESCREVA BEM RESUMINDO NO ESPAÇO ABAIXO​

Resposta:

2

Explicação passo-a-passo:

[tex]48 \div 24 = \\ \\ \frac{48}{24} = \\ \\ \frac{24}{12} = \\ \\ \frac{12}{6} = \\ \\ 2[/tex]

.

Esperamos ter ajudado! Bons estudos! Se merecermos, marque como melhor resposta para nos ajudar♥️

Resposta:

2

Explicação passo a passo:

primeiramente  metade

48/24

obtemos

24/12

metade novamente e obtendo

12/6

metade novamente

6/3

finalmente a terça que seria 2

Resposta: 15 = 59

Explicação:

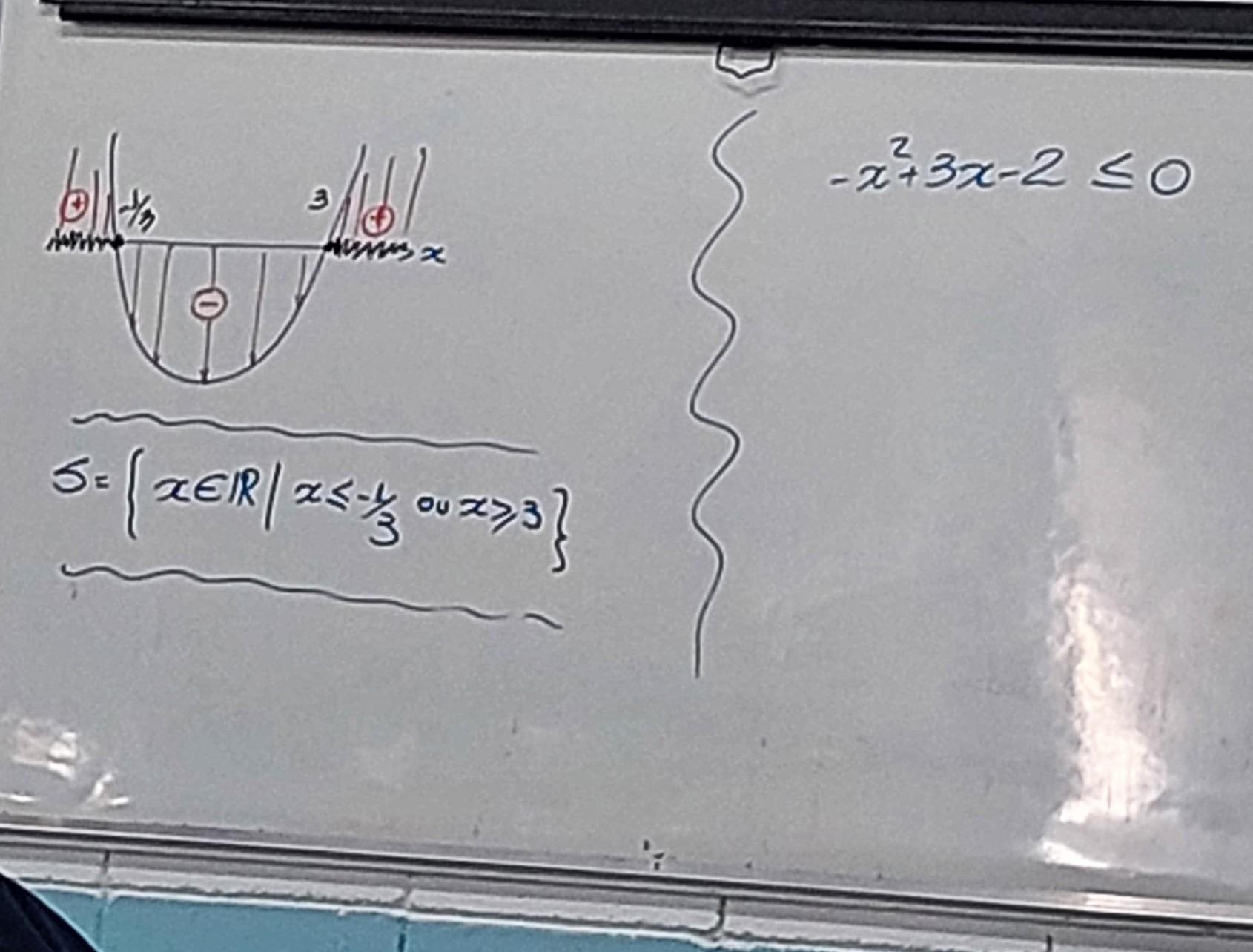
Resposta:

[tex]x=\mathbb{R}-(1,2)[/tex]

Explicação passo a passo:

[tex]-x^2+3x-2\leq0[/tex]

Quando a gente tem as inequações, a gente geralmente resolve a equação e vê onde ta satisfazendo, nesse caso

[tex]-x^2+3x-2=0[/tex]

que a gente pode resolver por bhaskara

[tex]-x^2+3x-2=0\\\\a=-1, b=3, c=-2\\\\x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\x=\frac{-3\pm\sqrt{3^2-4(-1)(-2)}}{2(-1)}\\\\x=\frac{-3\pm\sqrt{9-8}}{-2}\\\\x=\frac{3\pm\sqrt{1}}{2}\\\\x=\frac{3\pm1}{2}\\\\x={1,2}[/tex]

ou seja, em [tex]x=1[/tex] e [tex]x=2[/tex] temos valida a igualdade, vamos testar agora para um valor que seja menor que [tex]1[/tex], para facilitar contas vamos de [tex]0[/tex]

[tex]-(0)^2+3(0)-2=-2[/tex]

então para [tex]x < 1[/tex] temos satisfeita a inequação, vamos testar para valores entre [tex]1[/tex] e [tex]2[/tex], nesse caso o [tex]1,5[/tex]

[tex]-(1,5)^2+3(1,5)-2=-2,25+4,5-2=0,25[/tex]

Então para [tex]x[/tex] entre [tex]1[/tex] e [tex]2[/tex], ou seja, [tex]x\in(1,2)[/tex] não temos satisfeita a inequação, vamos testar agora para [tex]x > 2[/tex], para facilitar contas vamos de [tex]3[/tex]

[tex]-(3)^2+3(3)-2=-9+9-2=-2[/tex]

então para [tex]x > 2[/tex] temos satisfeita a inequação.

Juntanto todas as informações temos que [tex]x[/tex] satisfaz a inequação para quase todos os numeros reais, com exceção dos números no intervalo aberto [tex](1,2)[/tex], então podemos escrever a solução dessa inequação como

[tex]x=\mathbb{R}-(1,2)[/tex], ou seja, todos os numeros reais, menos o intervalo [tex](1,2)[/tex] aberto