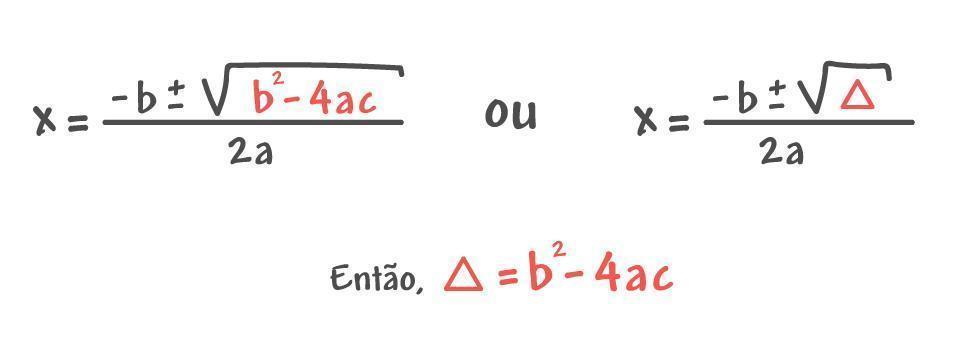Procedimento médico que colhe amostra de tecidos

Após calcular o valor de [tex]\Delta\\[/tex], verificou-se que a equação possui duas raízes reais, que corresponde a alternativa C.

Para verificar se a equação dada possui ou não raízes, calcula-se o valor de [tex]\Delta = b^2 - 4.a.c\\[/tex]

[tex]a = 1\\b = -2\\c = -1\\[/tex]

[tex]\Delta = b^2 - 4.a.c\\\\\Delta = (-2)^2 - 4.1.(-1)\\\\\Delta = 4 + 4\\\\\Delta = 8\\\\[/tex]

Como [tex]\Delta \\[/tex] é maior que zero, a equação admite duas soluções reais.

Veja mais em:

https://brainly.com.br/tarefa/41074590

https://brainly.com.br/tarefa/46283298

A equação em questão possui duas soluções reais.

[tex]\large\boxed{\textsf{\textbf{Alternativa~correta $\Rightarrow$ C}}}[/tex]

Temos três possíveis casos para o quantitativo de raízes reais para equações do segundo grau:

• Nenhuma raiz: [tex]\sf \Delta < 0 \Rightarrow x_{1}\:e\:x_{2} \notin \mathbb{R}[/tex]
• Uma raiz real: [tex]\sf \Delta = 0 \Rightarrow x_{1} = x_{2} \in \mathbb{R}[/tex]
• Duas raízes reais distintas: [tex]\sf \Delta > 0 \Rightarrow x_{1} \neq x_{2} \in \mathbb{R}[/tex]

Podemos efetuar o cálculo através da discriminante, e de forma simplificada, encontrar o que procuramos (nº de raízes):

[tex]\large\text{$\sf \Delta = b^{2}-4ac$}[/tex]

Temos os coeficientes:[tex]\begin{array}{l}\bullet\sf~A=1\\\bullet\sf~B=-2\\\bullet\sf~C=-1\\\end{array}[/tex]

Basta substituir na discriminante:

[tex]\begin{array}{l}\sf \Delta = b^{2}-4ac\\\sf \Delta = (-2)^{2}-4\times1\times(-1)\\\sf \Delta = 4-4\times(-1)\\\sf \Delta = 4+4\\\large\boxed{\bf \Delta=8}\end{array}[/tex]

Como, Δ é maior que zero, temos duas raízes reais para a equação.

◉ brainly.com.br/tarefa/50960413

◉ brainly.com.br/tarefa/47318533

Dúvidas? Estarei a disposição para eventuais esclarecimentos.

[tex]\begin{array}{l}\textsf{\textbf{Bons\:estudos!}}\\\\\text{$\sf Sua\:avaliac_{\!\!,}\tilde{a}o\:me\:ajuda\:a\:melhorar$}~\orange{\bigstar\bigstar\bigstar\bigstar\bigstar}\\\textsf{Marque\:como\:a\:melhor\:resposta\:\textbf{se\:for\:qualificada}}\\\\\textsf{\textbf{\green{Brainly}}\:-\:\blue{\sf Para\:estudantes.\:Por\:estudantes}}\end{array}[/tex]

A música de Belchior, "Como nossos pais" é algo mais voltado para o socialismo, pelo fato de dizer que por muito tempo eles sonharam em mudar a realidade, mas acabaram vivendo que nem os mais, os conservadores.

De acordo com o socialismo as pessoas viveriam em uma igualdade, onde todos teriam acesso a educação, saúde e bem estar.

 A música deixa claro que as pessoas buscam por dias melhores, mas esses dias melhores, no caso o socialismo, não acontece com tanta facilidade, parece uma utopia.

 Leia mais sobre o socialismo em: https://brainly.com.br/tarefa/5160420

Resposta:

significado de casas etimologia ( origem da palavra casas ) . a palavra casas deriva como plural de casa está derivada do latim casa, ae

" , com o sentido de cabana

explicação

Resposta:

Casas

Explicação:

O plural de casa é casas

Resposta:

Seria alternativa ''B''

Explicação:

A Constituição de 1988 estabelece a prevalência dos direitos humanos como princípio do Estado brasileiro em suas relações internacionais. ESPERO QUE TENHA AJUDADO!

Resposta:

A Constituição de 1988 estabelece a prevalência dos direitos humanos como princípio do Estado brasileiro em suas relações internacionais.

Explicação: